>>Return to Tell Me About Statistics!
In Vol.4, we explain how to calculate the number of n (sample size) required when conducting a questionnaire survey (market survey or social survey) targeting local residents and patients.
This article describes the number n (sample size) required to conduct clinical trials.
The concept of setting the number of n (sample size) when designing a clinical research plan
Clinical trials should be conducted with as few subjects as possible to reduce the burden on subjects and the cost of clinical trials. However, if there are too few subjects, the confidence interval becomes too wide owing to the large standard error, and the effect of the treatment may not be detected as a result of the clinical trial. However, if there are too many participants, the width of the confidence interval for the population may be too narrow to detect medically meaningful results.
Therefore, setting the number of n (sample size) to show medically meaningful results with as few subjects (number of cases) as possible is important.
Two possibilities to be wrong in the test results
One mistake that must be avoided in clinical trials is judging an ineffective treatment as effective.
Such a mistake is called “the typeⅠerror.”
The type Ⅰ error is also called “α-error.” This is an error in rejecting the null hypothesis (that the new treatment has the same effect as the conventional treatment), although it is correct.
This is more likely to occur when the sample size (n) is large. This α is the significance level.
Another mistake is stopping a clinical trial because one judges an effective treatment as ineffective. This mistake is called “the type II error.”
The type II error is called “β error,” which is the error of missing the null hypothesis when it is wrong.
This was more likely to occur when n (sample size) was small.
For researchers conducting clinical trials, β errors should be avoided as much as possible.
Power is defined as ” 1-β” and is the probability that a treatment will be considered effective.
Set the number of n (sample size)
Setting the number of n (sample size) in a clinical trial requires values for the ” significance level,” “power,” and “the size of the treatment effect you wish to detect.”
A significance level (α) of 0.05 or 0.01 is often used, and power (1-β) is set between 0.8 and 0.9. Therefore, only the “size of the treatment effect (effect size)” must be calculated.
The size of the treatment effect (effect size) is the extent to which an effect is set based on past clinical trial data and preliminary trial data. For example, the possible outcomes of a clinical trial are estimated before the trial begins, such as the mean difference in blood pressure of 8 mmHg between new and existing treatments.
If the effect is large, the n (sample size) must be small; if the effect is small, the n (sample size) must be large. For example, if the effect is halved, the required number n (sample size) is quadrupled.
If the variability (standard deviation) of the data obtained in a clinical trial is small, the number of samples n (sample size) will also be small. However, if the data variability is large, the required number n (sample size) is large. For example, if the standard deviation is doubled, the required number n (sample size) is quadrupled.
How to calculate the actual number of n (sample size)
The actual number n (sample size) can be calculated using different mathematical formulas, depending on the test method used to determine the results of a clinical trial.
One thing to note is that the international guideline “Consolidated Standards of Reporting Trials Statement” requires that the article summarizing the study results describe how the number of n (sample size) was determined when the study was designed. The “Consolidated Standards of Reporting Trials Statement” stipulates that papers summarizing research results should state how the n-number (sample size) was determined when the research was designed. Therefore, once n (the sample size) is determined, it cannot be easily changed.
An example of how to calculate the actual number of n (sample size) (test of population mean)
The value of the test statistic was strongly influenced by sample size (number of samples) and power. In general, the larger the sample size and power, the larger the value of the test statistic. Conversely, the smaller the sample size and power, the smaller the value.
Even if the null hypothesis m = m0 and there is a meaningful difference between m and m0, if the sample size or power is small, the value of the statistic|t0| will not be large, and the result will be “no significant difference.” Conversely, even if the difference between m and m0 was small, it was significant if the sample size or power was large.
It is dangerous to rely on such test results.
Therefore, it was necessary to verify the test again after setting the sample size and power.
[Calculation Method]
This section explains the determination of sample size when the null hypothesis (H0: m=m0) and the alternative hypothesis (H1:m≠m0) in the test of the population mean.
Suppose that we wanted to reject H0 with a power(1-β) for a significance level (α) when the quantity that indicates how many times the difference between the value m0 and the true m is the population standard deviation (σ) under the null hypothesis is|Δ|≥Δ0>0 (effect size:Δ = (m – m0)/σ).
The formula for setting the sample size n needed to do so is as follows:
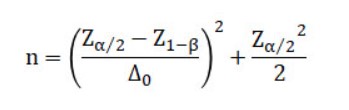
[Example]
Compute a test of the population mean, where the significance level (α) is 0.05, the null hypothesis (H0: m=m0), and the alternative hypothesis (H1: m ≠ m0). If we want to reject H0 with Δ=(m – m0)/σ≥Δ0=1.0 and power(1-β)=0.90, how many sample sizes are needed?
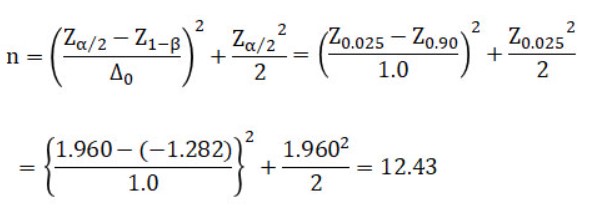
※Z=Values in the table of standard normal distribution
Thus, the candidate sample size is n = 13 or n = 12.
This article discusses the sample sizes (n) required for clinical trials. When reading articles on clinical trials, we must check the primary endpoints ,their statistical and the sample size calculate methods.
>>Return to Tell Me About Statistics!


Comments are closed